Elliptic Curve Cryptography for Beginners

Note: I no longer think that this is an ideal way to learn or understand elliptic curves. While you won't learn anything incorrect from this post, this doesn't reflect my current ideas about pedagogy, and I hope to write a updated post at some point.

I find cryptography fascinating, and have recently become interested in elliptic curve cryptography (ECC) in particular. However, it's not easy to find an introduction to elliptic curve cryptography that doesn't assume an advanced math background. This post is an attempt to explain how ECC works using only high school level math. Because of this, I purposely simplify some aspects of this, particularly around terms that have specific mathematical meaning. However, you should still get a good intuitive understanding of elliptic curves from this post.

The fundamental building block of most modern cryptography is a one-way function. A one-way function is a function that is easy to compute, but its inverse is hard¹ to compute. (i.e. given \(f(x) = y\), it's easy to calculate \(y\) given \(x\), but hard to calculate \(x\) given \(y\).)

There are two main ways that this is done:

1. Factorization
2. Elliptic Curve Logarithms

This post will focus on how elliptic curves can be used to provide a one-way function.

First, let's define an elliptic curve. An elliptic curve is defined by the function:

\[y^2 = x^3+ax+b\]

Where \(a\) and \(b\) are parameters of the curve. The constraint that \(4a^3 + 27b^2 \neq 0\) is also imposed to eliminate curves that have cusps or self-intersections.

Here's a interactive graph of what this looks like:

a:

b:

For examples of cusps and self-intersections, try \(a = 0; b = 0\) or \(a = -3; b = 2\), respectively.

That demo works on real numbers, but in actuality, you can define an elliptic curve over any field. A field is a set of objects that have addition, subtraction, multiplication, and division defined on them. For example, the real numbers (\(\mathbb{R}\)) are a field. In cryptography, we usually use the field "integers mod p" (\(\mathbb{Z}\bmod p\)), where \(p\) is a large prime number. I will continue to use the real numbers for the rest of this post, but know that all of the math is transferable to \(\mathbb{Z}\bmod p\), which is what is used in real crypto systems.

Now that you know what an elliptic curve is, let's talk about the points on it. We can define a group of the points on the elliptic curve. A group is a set of objects that have addition defined on them².

For points on the curve, we can define the addition operation geometrically like this:

To add two points, \(A\) and \(B\), draw a line through points \(A\) and \(B\), and label the third intersection with the line and the curve \(C\). We define addition such that \(A + B = -C\).

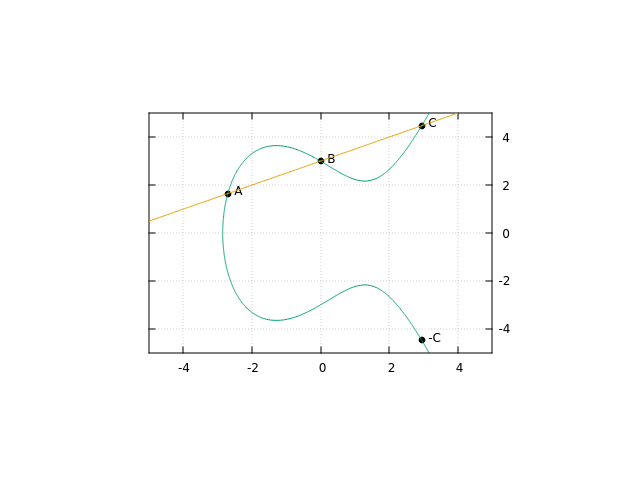
One question that comes up with this approach is what happens if there is no point \(C\) on the curve? For example, if \(B = -A\), we will never have another point on the curve. For this case, we simple define a point \(0\) (often referred to as the "point at infinity"), and say that if there is no other point \(C\), then \(A + B = 0\). This also fits with our algebraic intuition of what 0 should be, since the only case where \(A + B = 0\) is when \(B = -A\).

The other question that comes up is what should happen in the case that \(A = B\)? In this case, we simply take the line tangent to the curve at \(A\), and use that instead of the line going through \(A\) and \(B\).

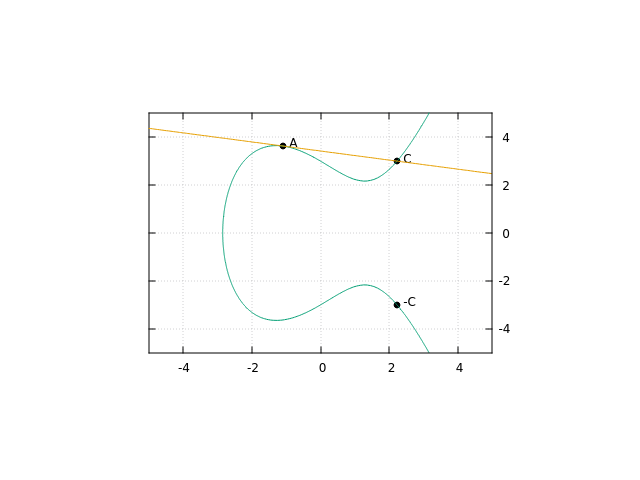
In doing this, we also define multiplication of a point on a elliptic curve - Since \(A + A = 2A\), we can simply repeatedly add the same points in order to multiply by an arbitrary number. (There are more efficient algorithms than this³, but those are beyond the scope of this article)

Now that you know what elliptic curves are, let's loop back around to our original goal: creating a one way function.

We've actually already done this: multiplication of points on an elliptic curve by a scalar is easy, but finding the scalar given the original point and the result of the multiplication is very difficult⁴. This is known as the Elliptic Curve Discrete Logarithm Problem⁵.

If \(Al = Q\), finding \(Q\) given \(A\) and \(l\) is easy, but finding \(l\) given \(A\) and \(Q\) is hard. (in this case, \(A\) and \(Q\) are points on the curve, \(l\) is an integer).

And there we have a one way function!

Thanks to Julian Squires, Harrison Clarke, George Tankersley, Laura Peskin, and Will Turner for comments/feedback/discussion.